intégrable

intégrable [ ɛ̃tegrabl ] adj.

• 1704; de intégrer

♦ Math. Qui peut être intégré. Fonction intégrable, qui admet une intégrale. Équation différentielle intégrable, qui admet des solutions.

● intégrable adjectif Se dit d'une fonction numérique d'une ou de plusieurs variables, qui admet une intégrale. (Les classes importantes de fonctions intégrales sur une partie de R sont les fonctions monotones, les fonctions continues, les fonctions bornées et continues par intervalles sur un segment [a,b], les fonctions en escalier.)

intégrable

adj. Que l'on peut intégrer.

|| MATH Dont on peut calculer l'intégrale (fonctions).

⇒INTÉGRABLE, adj.

Qui peut être intégré. Groupe intégrable. La différence des coûts régionaux de la vie n'y est pas intégrable (PERROUX, Écon. XX^e s., 1964, p. 204).

— MATH. Fonctions intégrables :

• En continuant indéfiniment la subdivision de l'axe des temps en segments de plus en plus petits et tendant vers zéro, il peut se faire que les résultats obtenus tendent vers une limite finie. On dit alors que la fonction considérée est intégrable au sens de Riemann. Sinon, on dit qu'elle n'est pas intégrable.

Gds cour. pensée math., 1948, p. 288.

Prononc. : [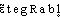]. Étymol. et Hist. 1704 math. (Trév., s.v. intégral). Dér. de intégrer; suff. -able.

DÉR. Intégrabilité, subst. fém. Caractère de ce qui est intégrable. Les conditions d'intégrabilité doivent donc être remplies (H. POINCARÉ, Électr. et opt., 1901, p. 609). La forme donnée par Riemann à la condition d'intégrabilité suggérait l'idée de « mesure » pour l'ensemble des points de discontinuité d'une fonction dans un intervalle (BOURBAKI, Hist. math., 1960, p. 249). — [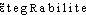]. — 1^re attest. 1873 (Lar. 19^e); de intégrable, suff. -(i)té.

intégrable [ɛ̃tegʀabl] adj.

ÉTYM. 1704; de intégrer.

❖

♦ Didact. (math.). Qui peut être intégré, dont on peut faire l'intégration. || Fonction intégrable.

❖

DÉR. Intégrabilité.

Encyclopédie Universelle. 2012.